Linear programming or Linear Optimization is mathematical modeling technique in which a linear function is maximized or minimized when subjected to various constraints. It is part of Operations Research (OR).
Business Problems are typically about maximization of certain goals (like revenue, or profit or both, production) or minimization of certain goals (like cost) in presence of constraints (like availability, capacity, time).
Hence the goal is to formulate a business problem or any such real world problem to a mathematical model and use linear optimization for obtaining the most optimal solution for the problem with given constraints. This technique has been useful for guiding quantitative decisions in business planning, in engineering, or social and physical sciences.
The most important parts are an objective function, linear inequalities with subject to constraints.
Formulation of the problem
The solution of a linear programming problem reduces to finding the optimum value (maximum or minimum) of the linear expression (called the objective function)
The steps involved are
Depict the linear expression or Objective Function
like
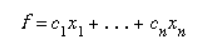
This is the objective function which has to be optimized
Depict the set of constraints expressed as inequalities:
like
The constants (a’s, b’s) are determined by the capacities, needs, costs, profits etc., and other requirements and restrictions of the problem.
The basic assumption of this method is that the various relationships between demand and availability are linear; that is, none of the xi is raised to a power other than 1.
In order to obtain the solution to this problem, it is necessary to find the solution of the system of linear inequalities (that is, the set of n values of the variables xi that simultaneously satisfies all the inequalities).
Once the problem is solved for all inequalities - The objective function is then evaluated by substituting the values of the xi in the equation that defines f.
Solving this becomes complex as the number of variables xi increase and the constraints become more complex. Computing power can be used here.
MS Excel Solver
Microsoft's Excel Solver Add-In reduces the time to solve the problem by performing the calculations to solve the inequalities, provided we well identify the objective function and constraints or inequalities.
To know more about Excel Solver